Welcome back to the WebRef.org blog. We have decoded the power structures of political science and the massive engines of macroeconomics. Today, we look at the mathematical “glue” that holds all these disciplines together: Statistics.
In 2025, statistics is no longer just about calculating averages or drawing pie charts. It has become a high-stakes, computational science focused on high-dimensional data, automated decision-making, and the ethical pursuit of privacy. Here are the defining topics in the field today.
1. Causal Inference: Moving Beyond Correlation
The old mantra “correlation does not imply causation” is finally getting a formal solution. Causal Inference is now a core pillar of statistics, using tools like Directed Acyclic Graphs (DAGs) and the Potential Outcomes Framework to determine why things happen, rather than just noting that two things happen together.
This is critical in medicine and public policy where randomized controlled trials (the gold standard) aren’t always possible. By using structural equation modeling, statisticians can “control” for variables after the fact to find the true impact of a new drug or a tax change.
2. Synthetic Data and Privacy-Preserving Analytics
As data privacy laws become stricter globally, statisticians have turned to a brilliant workaround: Synthetic Data. Instead of using real customer records, algorithms generate a completely fake dataset that has the exact same statistical properties as the original.
This allows researchers to study patterns—like disease spread or financial fraud—without ever seeing a single piece of private, identifiable information. This often goes hand-in-hand with Differential Privacy, a mathematical technique that adds a calculated amount of “noise” to data to mask individual identities while preserving the overall trend.
3. Bayesian Computation at Scale
Bayesian statistics—the method of updating the probability of a hypothesis as more evidence becomes available—has seen a massive resurgence. This is due to breakthroughs in Probabilistic Programming and Markov Chain Monte Carlo (MCMC) algorithms that can now handle billions of data points.
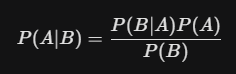
This approach is vital for Uncertainty Quantification. In 2025, we don’t just want a single “best guess”; we want to know exactly how much we don’t know, which is essential for autonomous vehicles and high-frequency trading.
4. Edge Analytics and IoT Statistics
With billions of “smart” devices (IoT) generating data every second, we can no longer send all that information to a central server.2 Edge Analytics involves running statistical models directly on the device—the “edge” of the network.
Statisticians are developing “lightweight” models that can detect a failing factory machine or a heart arrhythmia in real-time, using minimal battery power and processing strength.
5. High-Dimensional and Non-Stationary Time Series
In the era of 6G networks and high-frequency finance, data moves too fast for traditional models. Researchers are focusing on Long-Range Dependence (LRD) and the Hurst Exponent ($H$) to understand “memory” in data streams. This helps predict persistent trends in climate change and prevents crashes in volatile markets where the “random walk” theory fails.
Why Statistics Matters in 2025
Statistics is the gatekeeper of truth in an age of misinformation. Whether it is verifying the results of an AI model, auditing an election, or tracking the success of a climate initiative, statistical rigor is what separates a “guess” from a “fact.”
